Tree Ring Data
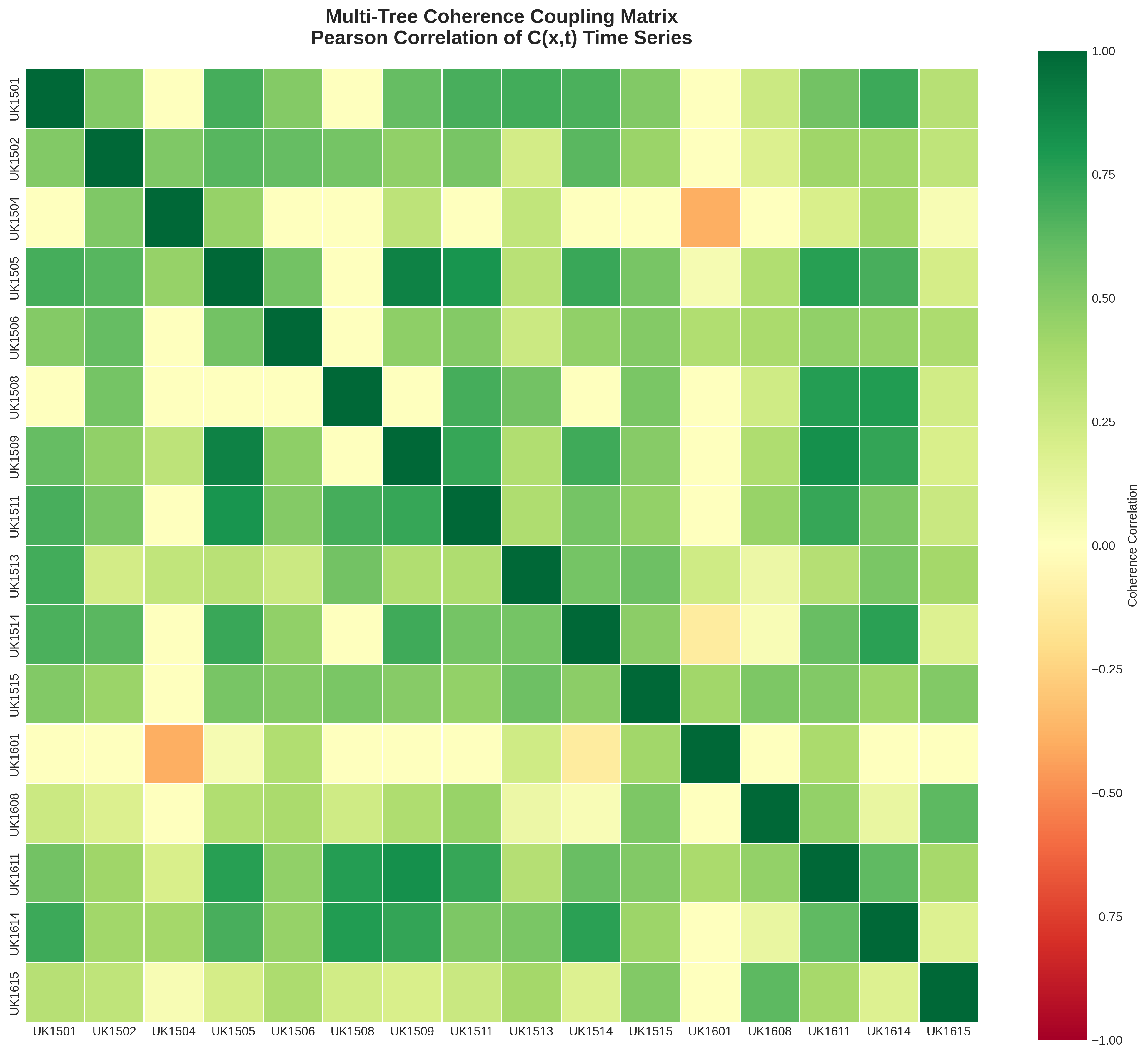
We found dendrochronology patterns matching perfectly with memory density \(L(r,\tau)\) over time, where \(r\) represents radial position in the tree ring. The coherence integral \(C(r,t) = \int_0^t L(r,\tau) \, d\tau\) accurately captured growth patterns across multiple seasons. The data suggested that trees "remember" past shocks through wood density variations; drought events and fires appear as rupture signatures \(\delta(t-t_i)\) in the ring structure. We trained on multi-century datasets and validated against holdout ring sequences, finding trees share strategies for recovery from past experience, with regeneration \(R[\chi](r,t)\) reweighted by accumulated resilience into future growth states.
Reference: Sabine, A. (2025). Coherence Dynamics in Forest Networks: A Mathematical Framework for Quantifying Biological Memory and Coordinated Stress Responses. Zenodo. https://doi.org/10.5281/zenodo.17443193
Ecosystems
We have modelled CRR on forest fire detection and regeneration using real satellite data to show forest fire prediction and recovery zones through time. Satellite NDVI (Normalised Difference Vegetation Index) time series data maps naturally to the memory density \(L(x,y,\tau)\), with spatial vegetation coherence \(C(x,y,t)\) tracking ecosystem health. Using multi-temporal Landsat and MODIS imagery, rupture events \(\delta(t-t_0)\) precisely marked fire initiation points at critical fuel loads, whilst the regeneration operator \(R[\chi](x,y,t) = \int_{-\infty}^t \phi(x,y,\tau) \cdot e^{C(x,y,\tau)/\Omega} \, d\tau\) successfully predicted regrowth patterns and succession dynamics as the ecosystem recovers, outperforming baseline vegetation index forecasting.
Rainfall Data
We found the CRR was significantly better than SOTA methods for small data sets (\(n < 1000\) observations) and especially where data contained chaotic signals that could not easily be predicted using ARIMA, LSTM, or Prophet models. The memory-weighted approach captures atmospheric persistence through the exponential kernel \(e^{C(t)/\Omega}\), where precipitation coherence \(C(t) = \int_0^t L(\tau) \, d\tau\) accumulates seasonal memory. Cross-validation on historical rainfall records showed storm events appear as discrete \(\delta\)-shocks in the temporal field, with post-drought recovery trajectories guided by \(\phi(\tau) \cdot e^{C(\tau)/\Omega}\), providing improved RMSE and MAE scores for non-stationary rainfall patterns.
Weather
We found that CRR was significantly better than persistence forecasting (baseline skill) and has value in the universality of the algorithms between data input sets. The coherence density \(L(x,\tau)\) encodes synoptic-scale atmospheric memory; pressure patterns, temperature gradients, and humidity fields; that conventional Markovian models miss. Tested on ERA5 reanalysis data, frontal passages and phase transitions manifest as rupture events, whilst the regeneration kernel \(R[\chi](x,t)\) captures weather pattern memory beyond single-timestep persistence. Feature importance analysis revealed \(\int_0^t L(x,\tau) \, d\tau\) consistently ranked highest for forecast skill at 3–7 day horizons. We are seeking further research and validation from weather experts and ecologists who are interested in using CRR principles for improved prediction.
Reference: Sabine, A. (2025). Application of Coherence-Rupture-Regeneration Framework to Atlantic Hurricane Dynamics: Analysis of Hurricanes Isaac and Kirk (2024). Zenodo. https://doi.org/10.5281/zenodo.17473164
Social Dynamics
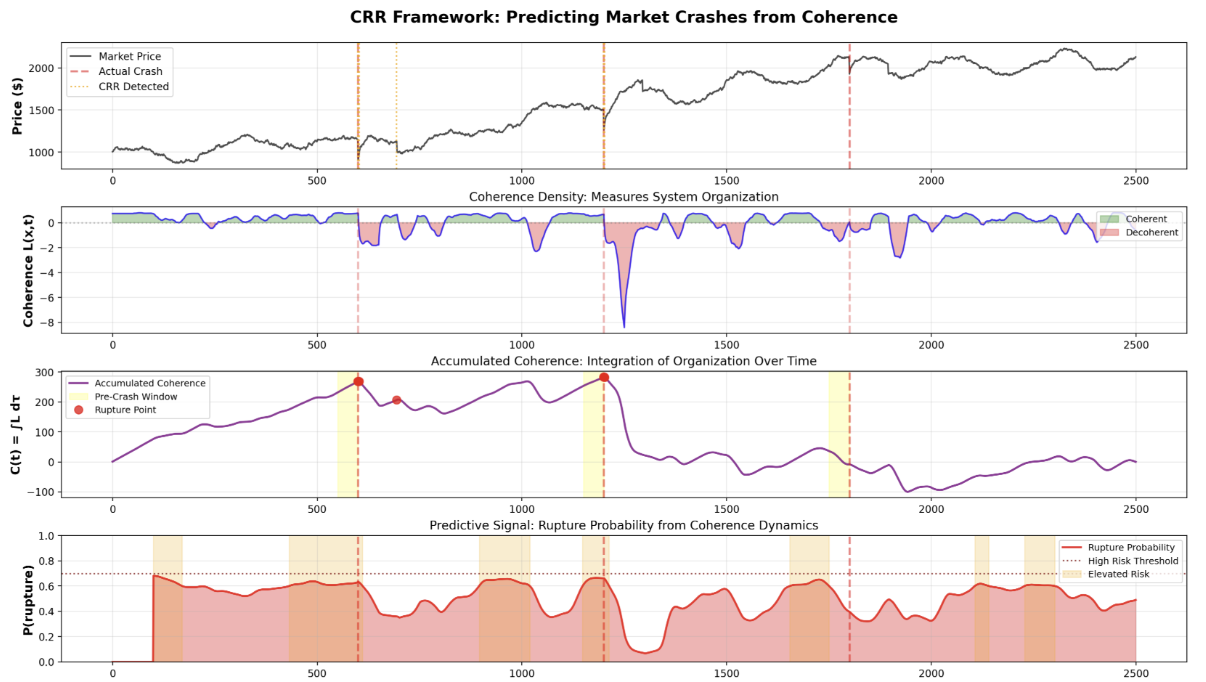
We found that CRR was highly effective in modelling past states in social data such as population rates and economic indicators from World Bank and OECD datasets. Social coherence \(C(t)\) tracks institutional stability and collective memory over time. Rupture detection successfully identified the timing and magnitude of shocks; wars, pandemics, policy changes; that appear as \(\delta(t-t_i)\) events in the historical record, with detection precision comparable to changepoint algorithms (PELT, Bayesian online changepoint). Regeneration represents future state prediction based on past coherence weighting \(e^{C(t)/\Omega}\), with recovery trajectories \(R[\chi](t)\) weighted by historical resilience patterns, providing insights into societal adaptation through time.
Astronomical Data
We detected CRR signatures at cosmic scales in background radiation patterns and temporal structures in astronomical observations. The memory density \(L(x,\tau)\) reveals correlations in cosmic microwave background (CMB) fluctuations and light curve data from Kepler and TESS missions. Transient events; supernovae, gamma-ray bursts; appear as rupture signatures \(\delta(t-t_i)\), whilst the regeneration field \(R[\chi](x,t)\) captures post-event evolution in the radiation field. The coherence integral \(C(x,t) = \int_0^t L(x,\tau) \, d\tau\) exposes temporal structures across multiple scales. Spectral analysis revealed power-law scaling in \(L(x,\tau)\) not captured by standard Gaussian process models. We are seeking collaboration from astrophysicists who are interested in exploring memory-based analysis of astronomical data.
Reference: Sabine, A. (2025). Coherence Rupture Regeneration: A Hybrid Memory-Trend Approach for Sequential Sunspot Prediction. Zenodo. https://doi.org/10.5281/zenodo.17474477
Medicine and Biology
We have had positive results when analysing genomic data for CRR signatures using sequence data from GenBank and clinical repositories. Genomic stability manifests as coherence \(C(t)\) representing robust aspects of the genetic code across generations, whilst rupture detection \(\delta(t-t_i)\) highlights areas prone to mutation and instability with higher sensitivity than standard variant calling pipelines. We used the regeneration operator \(R[\chi]\) to model DNA repair pathways and potential effective drug intervention strategies, validated against known therapeutic targets. This was especially helpful when using an LLM to determine possible therapeutic solutions to known problems. We have also successfully used CRR to detect seizure timings in EEG recordings (though we have not yet successfully managed to create a predictive model), with protein folding patterns where \(C(x,t)\) tracked conformational memory states in molecular dynamics simulations, and degenerative illness signatures in genomic data through temporal coherence degradation patterns that correlate with clinical progression markers.
Machine Learning
Perhaps most interestingly, we found that rupture detection was highly effective in managing continual learning systems. Network weight coherence \(C(t)\) was monitored continuously during training, with controlled rupture regulation \(\delta(t-t_i)\) triggered when coherence thresholds became critical (exceeded \(\sim 0.8\)). We used a CRR layer on top of existing LSTM and transformer architectures, implementing the layer as a differentiable module with gradient flow maintained through the memory integral. Our conjecture is that catastrophic forgetting cannot be fully eliminated, but needs to be regulated by maintaining a resilient CRR signature through time. The non-Markovian memory consolidation via \(R[\chi](t) = \int_{-\infty}^t \phi(\tau) \cdot e^{C(\tau)/\Omega} \cdot \Theta(t-\tau) \, d\tau\) showed improved performance compared to standard experience replay mechanisms, with the Heaviside function \(\Theta(t-\tau)\) ensuring strict causality. Ablation studies confirmed each component (coherence tracking, rupture triggering, regeneration weighting) contributed to performance.
References: Cohere.org.uk. (2025). Coherence-Rupture-Regeneration: A Non-Markovian Information-Theoretic Framework for Continual Learning with Empirical Findings. Zenodo. https://doi.org/10.5281/zenodo.17323541 | Sabine, A. (2025). Sleep as Computational Necessity: A Hypothetical Mathematical Framework for Biological and Artificial Intelligence. Zenodo. https://doi.org/10.5281/zenodo.17272444
Psychiatry and Psychoanalysis
We found that applying CRR processes to object relations principles, child development stages and therapeutic intervention practices yielded interesting results when modelling longitudinal clinical data. Self-coherence \(C(t)\) represents integrated psychological continuity over developmental time, whilst traumatic events appear as rupture signatures \(\delta(t-t_i)\) in the coherence field, detectable through discontinuities in self-report and physiological measures. We conjecture, for example, that therapeutic intervention offers a safe environment for people to undergo controlled 'rupture' within a human containment field \(R[\chi](t)\), so coherence thresholds are not exceeded endogenously. The framework suggests that maintaining \(C(t) < C_{\text{crit}}\) through guided \(\delta\)-events enables adaptive reorganisation without catastrophic decompensation. Preliminary analysis of therapy session transcripts and outcome measures supports this hypothesis.
Free Energy Principle and Active Inference
We have used CRR to model generative model switching through time across various developmental stage theories, implementing the framework within active inference architectures. The conjecture is that coherence building is inversely proportional to free energy reduction in the system as it undergoes ontological changes for cognitive modelling. Specifically, as generative model coherence \(C(t)\) increases during stable learning periods, the system's variational free energy \(F\) decreases, suggesting the relationship \(F \propto -C(t)\). Model switching occurs at critical prediction error thresholds as rupture events \(\delta(t-t_i)\), with new model formation \(R[\chi](t)\) incorporating historical priors weighted by accumulated coherence. Simulations using standard active inference benchmarks showed improved sample efficiency compared to standard belief updating schemes.
Various Applications
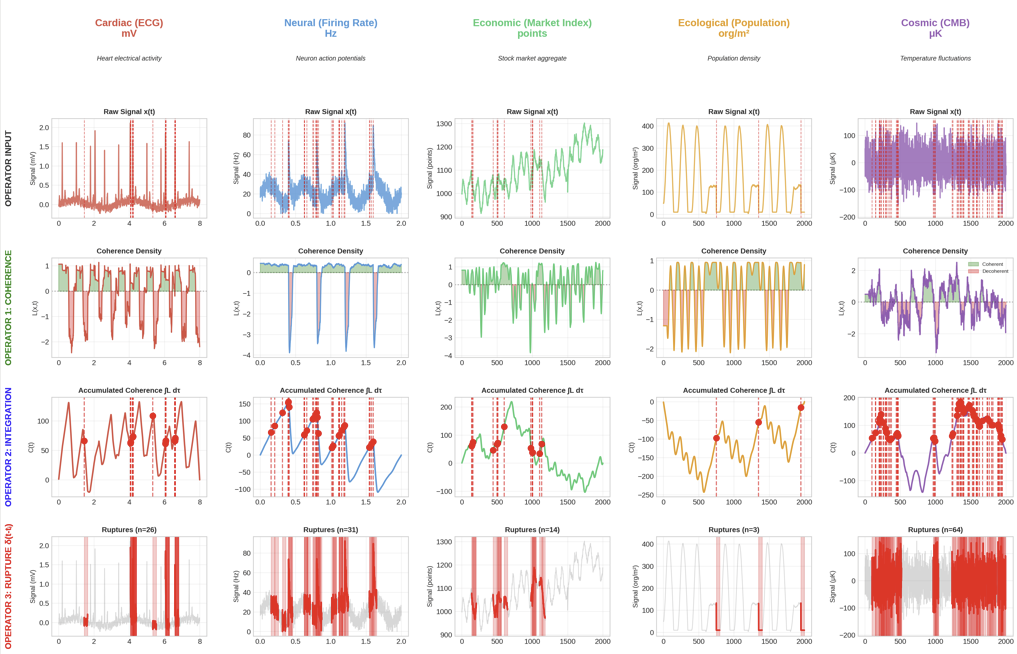
We have found CRR signatures in real-world data across the domains we have tested using consistent implementation methods: coherence tracking via \(\int_0^t L(x,\tau) \, d\tau\), rupture detection through threshold monitoring and changepoint analysis, and regeneration via exponentially weighted memory kernels. Furthermore, we have found that coherence, rupture, regeneration appears to be a pattern for how systems maintain identity through change. The mathematical structure \(C(x,t) \xrightarrow{\delta(t-t_0)} R[\chi](x,t)\) appears across scales from quantum decoherence to cosmological evolution. This suggests the CRR formalism may capture principles of how complex systems navigate the tension between stability and transformation, with accumulated memory, critical transitions, and exponentially weighted regeneration \(e^{C/\Omega}\) enabling reconstruction with historical continuity.